An interesting paper from Loïc Henriet, Quantum Engineer and Head of Software at Pasqal, Christophe Jurczak, General Partner at Quantonation and Leonard Wossnig, CEO of Rahko.
The original article was published in Medium.com on November 13th, 2019.
Machine Learning aims at automatically identifying structures and patterns in large data sets. In order to identify these patterns, algorithms often resort to standard linear algebra routines such as matrix inversion or eigenvalue decompositions. For example, support vector machines, one of the most successful traditional machine learning approaches for classification, can be cast to a linear system of equation, and then be solved using matrix inversion. Similarly, identifying the important signals in a data set can be done by identifying the leading eigenvalues and vectors of the data matrix, a method called principal component analysis. The large dimensionality of the vector spaces involved in these operations make their implementation at large scale very resource intensive, thus motivating the development of innovative methods to lower their computational cost.
A first wave
Researchers at MIT then proposed to use a quantum computer to perform these linear algebra routines more efficiently (see reviews [1],[2]). The key idea behind this proposal is that an ensemble of n quantum bits is described by a large 2ⁿ-dimensional complex vector, or quantum state, and operations/gates on these quantum bits by 2ⁿ times 2ⁿ dimensional matrices. By taking advantage of the exponential amount of information potentially encoded in an ensemble of n quantum bits, several quantum algorithms were devised that could potentially outperform state-of-the-art classical algorithms for these linear algebra tasks.
The discovery of these algorithms triggered a lot of research efforts at the intersection of machine learning and quantum computing, but the resource requirements for their implementation in terms of numbers of qubits and gate fidelities is unfortunately prohibitive for devices that are and will be available in the short term. Beyond these technological requirements, the main obstacle is the lack of an efficient protocol/device for encoding and accessing classical data into the quantum state, i.e. the need for a so-called quantum Random Access Memory. It is unclear today when such a device could be built and whether it would be cost-efficient. As a nice side effect, however, these results inspired novel classical methods [3] based on random subsampling of the data. Indeed, it was shown that using similar data access as in the quantum algorithms, we are also able to perform classical linear algebra routines exponentially faster on classical computers.
Noisy qubits and new applications
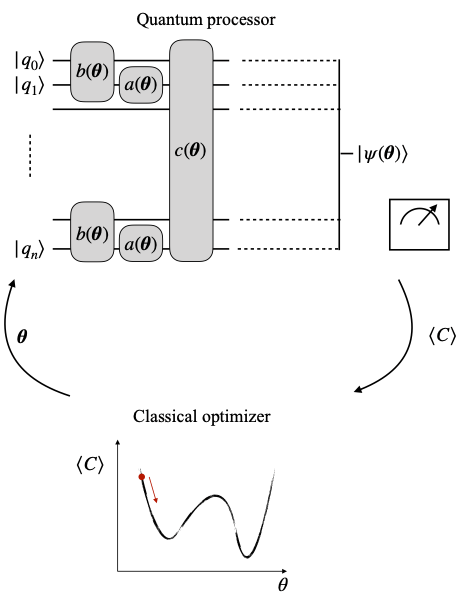
Motivated by these developments, people tried to find other ways to leverage Machine Learning methods on available quantum processors, albeit for other purposes than data intensive applications such as the ones mentioned above. The general aim of these methods is to optimize for a given objective function, and the key idea is to use both a quantum and a classical processor in conjunction, with only a minimal number of operations realized on the quantum processor. In this hybrid framework, the sole use of the quantum processor is to prepare a given quantum state, parameterized by a set of variational parameters. One then extracts from this state an estimate of the objective function through repeated measurements. This estimate is in turn used as the input to a classical optimization procedure, which returns new variational parameters to prepare the quantum state for the next iteration. This loop is repeated multiple times until some stopping criterium is fulfilled, or the optimization procedure converged. Then, a final estimate of the objective function is output.
In this framework, the quantum processor can be seen as a trainable quantum algorithm whose output is adapted variationally to best match the task under consideration. Importantly, the variational nature of the procedure renders these algorithms relatively resilient to errors, making them prime candidates for an implementation on Noisy Intermediate Scale Quantum (NISQ) devices [4]. The general principle of these hybrid quantum-classical algorithms is illustrated in Fig. 1.
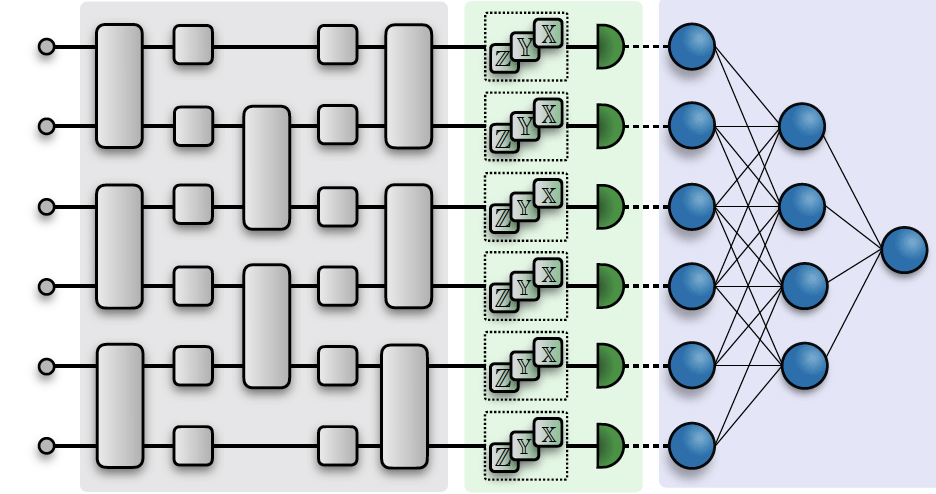
This approach, which bears similarities with classical neural networks, might lead to speedups for certain tasks thanks to the “exotic” correlations that can be encoded in the quantum state. The suitability of such quantum neural networks becomes evident when it comes to learning a complex quantum system, such as a molecule’s energy level in chemistry. As already Feynman pointed out mid last century, it seems natural to use a quantum system as a computational resource for quantum chemistry calculations. The potential applications in this field are tremendous. It could for example lead to a better understanding of enzymes-ligand interactions and discoveries of new drugs. In a similar vein, we could use this procedure to enhance our knowledge of complex many-body physics effects [5], such as Many-Body Localization or High-Temperature superconductivity. Beyond these fields, researchers are also actively exploring the use of quantum neural networks as classifiers [6] or for solving combinatorial optimization problems.
Hardware matters
In that respect, not all quantum hardware is equivalent, as the set of operations that can be natively implemented depend on the chosen qubit technology. One example notably includes the native resolution on a 2D platform of neutral atoms of a well-known graph problem, the Maximum Independent Set (MIS) problem. Considering an undirected graph composed of a set of vertices connected by unweighted edges, an independent set of this graph is a subset of vertices where no pair is connected by an edge. The objective of the MIS problem is to find the largest of such subsets. This problem, which has various applications in network design or finance, becomes hard to solve on a classical computer when the size of the graph grows.
The MIS problem can be tackled by using an ensemble of interacting cold atoms as a quantum resource, where each atom represents a vertex of the graph under study. As any quantum system, the dynamics of the atoms is governed by the Schrödinger equation, involving a Hamiltonian (energy functional) depending on the atomic positions, the electronic energy levels and their interactions. Interestingly, the physical interactions encoded in the Hamiltonian constrain the dynamics to only explore independent sets of the graph under study, then leading to an efficient search in the set of possible solutions [7], as illustrated in Fig. 2. This example underlines the prime importance of targeting the trainable quantum network to the specific task at hand, so that the class of trial quantum states that are generated represent good candidates for solving the problem under consideration.
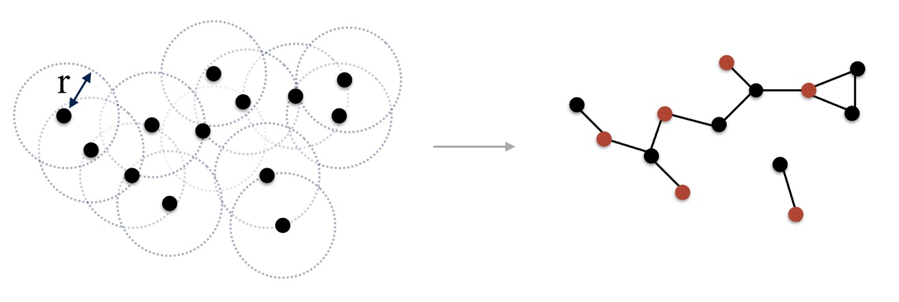
As such, gates fidelities or quantum volume are not always the best criteria for assessing the performances of a given quantum hardware on a specific task. Exploring the same phase space by using only standard quantum computing gates in a nearest-neighbor architecture would be far more demanding. Optimisation of resources according to adapted performance criteria for emerging quantum computing platforms is a topic for future research.
The way forward
The theoretical description of these systems is challenging, as we lack a complete theoretical understanding for such parameterized quantum circuits, similarly to classical neural networks. Additionally, most algorithms are of heuristic nature, and there is no efficient way to simulate larger quantum devices, which makes the analysis and understanding even harder. As such, no proof of a speed-up with respect to the best classical algorithms exists today.
Research is however progressing rapidly, and several key points have been identified to understand and enhance their performances:
- the choice of the parameterization determines the range of attainable solutions, which is generally a hard problem on its own.
- the second challenge is associated with the experimental difficulty of sampling enough repetitions of the quantum circuit to estimate accurately the objective function, which can seem prohibitive for some applications.
- another important point concerns the choice of the classical optimizer working in conjunction with the quantum processor, which is instrumental in exploring the parameter space and finding optimal solutions.
- finally, due to the imperfection of currently available quantum processors, one needs to set up techniques to mitigate the effect of errors.
All these aspects are the subject of active academic and industrial research and we understand better and better how each part of these quantum networks behave. For example, it has recently been shown how to compute the analytical gradient of the objective function with respect to the parameters [8]. Research has also led to the creation of classical optimizers specifically designed for quantum neural networks [9] as well as machine learning methods for lowering the sampling requirements [10] or explore the parameter space more efficiently [11].
As a conclusion, this whole new field, let’s call it Quantum Machine Learning, represents a powerful framework to describe and inspire activities in the field of algorithms development for NISQ machines. In that regard, the dynamism of the classical Machine Learning community could drive new advances in quantum Machine Learning, as the core concepts of the field are progressively adapted to the quantum domain.
To learn more
[1] J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe, S. Lloyd, Nature 549, 195–202 (2017).
[2] C. Ciliberto, M. Herbster, A. Davide Ialongo, M. Pontil, A. Rocchetto, S. Severini, L. Wossnig, Proceedings of the Royal Society A, 474, 2209, 20170551 (2018)
[3] E. Tang, Proceedings of the 51st Annual ACM SIGACT Symposium on Theory of Computing — STOC 2019, pp. 217–228 (2018) and arXiv: 1807.04271 (2018)
[4] J. Preskill, Quantum 2, 79 (2018).
[5] C. Kokail, C. Maier, R. van Bijnen, T. Brydges, M. K. Joshi, P. Jurcevic, C. A. Muschik, P. Silvi, R. Blatt, C. F. Roos, P. Zoller, Nature 569, 355 (2019). J. Eisert, M. Friesdorf, C. Gogolin, Nature Physics 11, 124 (2015).
[6] E. Grant, M. Benedetti, S. Cao, A. Hallam, J. Lockhart, V. Stojevic, A. G. Green, S. Severini, npj Quantum Information 4, 65 (2018).
[7] H. Pichler, S.-T. Wang, L. Zhou, S. Choi, and M. D. Lukin, arXiv:1808.10816 (2018). L. Henriet, arXiv:1910.10442 (2019).
[8] K. Mitarai, M. Negoro, M. Kitagawa, K. Fujii, Phys. Rev. A 98, 032309(2018).
[9]M. Ostaszewski, E. Grant, M. Benedetti, arXiv:1905.09692 (2019).
[10] G. Torlai, G. Mazzola, G. Carleo, and A. Mezzacapo, arXiv:1910.07596(2019).
[11] G. Verdon, M. Broughton, J. R. McClean, K. J. Sung, R. Babbush, Z. Jiang, H. Neven, M. Mohseni, arXiv:1907.05415 (2019)
