In Noisy Intermediate-Scale Quantum (NISQ) era, quantum processing units (QPUs) suffer from, among others, highly limited connectivity between physical qubits.
To make a quantum circuit executable, a circuit transformation process is necessary to transform it into a functionally equivalent one so that the connectivity constraints imposed by the QPU are satisfied.
While several algorithms have been proposed for this goal, the overhead costs are often very high, which degenerates the fidelity of the obtained circuits sharply. One major reason for this lies in that, due to the high branching factor and vast search space, almost all these algorithms only search very shallowly and thus, very often, only (at most) locally optimal solutions can be reached.
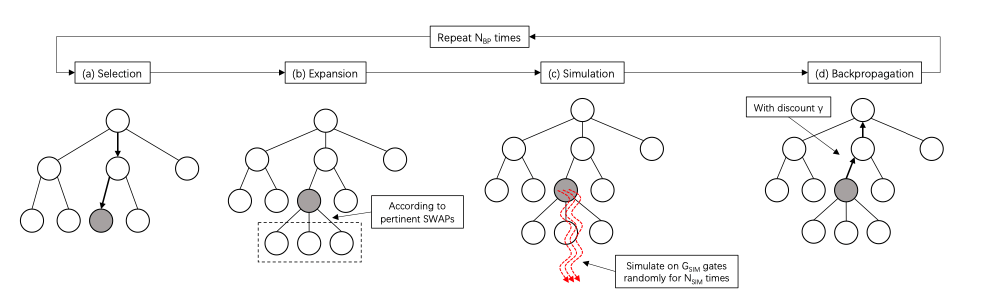
Researchers at Southeast University, China and University of Technology Sydney propose a Monte Carlo Tree Search (MCTS) framework to tackle this problem, which enables the search process to go much deeper.
In particular, they have designed, by taking both short- and long-term rewards into consideration, a scoring mechanism. and propose to use a fast random strategy for simulation.
The thus designed search algorithm is polynomial in all relevant parameters and empirical results on extensive realistic circuits show that it can often reduce the size of output circuits by at least 30% when compared with the state-of-the-art algorithms on IBM Q20.
The paper can be read there.
